摘要

本文的目的是研究非牛顿威廉森纳米流体流动的性质是如何受到热产生、粘性耗散和磁场的影响的，这种流动是由放置在多孔介质中的指数拉伸片引起的。本研究通过考虑温度对Williamson纳米流体导热系数和粘度的影响，重点分析传热过程。此外，研究这些纳米流体在滑移速度影响下的流动特性也有重要贡献。利用谱配点法(SCM)将描述当前问题的方程转化为常微分方程的集合，然后求解。本文提出的SCM主要依赖于apile型Changhee多项式(acp)的性质。首先，借助于acp，给出了近似函数导数的近似公式。通过这个过程，所提供的模型被转换成一组非线性代数方程。感兴趣的物理因素，如皮肤摩擦、努塞尔数和舍伍德数，用表格表达式来解释。数据以图形的形式显示纳米流体的速度、温度和浓度。初步结果表明，增大Williamson、磁性、导热系数和brown参数，可以显著改善热场。最后，用一些过去基于文献的出版物的具体案例来测试建议的方法，结果显示出良好的一致性。

1 介绍

由于牛顿流体模型的应用有限，非牛顿流体的研究引起了人们的兴趣。非牛顿流体包括淀粉、蜂蜜、番茄酱、润滑喷雾等物质。早先，人们提出了许多非牛顿流体模型。以此为基础，建立了威廉姆森模型。1929年，Williamson[1]提出了一个非牛顿流体模型来说明这些流体的流变特性。剪切变薄是非牛顿流体的一个特征，如Williamson流体模型。在文献中，Williamson流体模型是对流体在剪切作用下变薄的描述。由于威廉姆森模型在过去十年中在照明流体动力学方面的适用性，它已被许多研究人员使用(见[2-8])。

纳米技术由于其在工业领域的适用性，目前正引起科学家和研究人员的关注，例如应用纳米流体冷却核反应堆、调节热阀的热流、降低汽车散热器温度、冷却计算机处理器等。在医学领域，癌症患者使用由铁基纳米流体制成的装置提供的药物和辐射来治疗。Choi[9]通过将纳米级材料颗粒掺入常规流体中，建立了“纳米流体”的名称，并在数学上验证了该方法。纳米颗粒主要由金属、氮化陶瓷、氧化物陶瓷、碳化物陶瓷和常见的基础流体如甲醇、水、乙二醇和油组成。[10,11]作者的实验结果证明，纳米流体比普通流体具有更高的导热性。混合对流是流体流动同时涉及自然对流和强制对流机制的现象[12]。它在实际应用中具有重要意义，特别是在传热和流体动力学领域。它的意义在于它能够影响流体的流动模式，提高传热速率，提高能量效率，并影响热分层。混合对流现象的精确建模和分析对于优化不同行业中各种工程系统的效率和性能至关重要。由于混合对流的重要性，Abbaset等[13]在二年级的纳米流体流动研究中解决了这一现象。此后，许多作者(见[14-18])对纳米流体在各种热物理环境下的流动进行了广泛的调查。

在本文中，我们将首次借助apeltype Changhee多项式推导出导数的近似公式，并将其应用于利用谱搭配方法求解所研究的模型(参见[19,20])。这些方法最著名的优点是它们能够以非常小的自由度误差生成准确的结果[21]。由于它们在逼近函数方面具有良好的性质，因而得到了广泛的应用。利用acp的正交性来近似其域上的函数。这些多项式在ode的方法中起着重要的作用[22]。许多研究人员使用并实现了这些多项式来数值解决许多问题，例如在[23]中，它们被用于求解高维混沌洛伦兹系统。因此，本文的主要目标是研究非牛顿纳米流体的混合对流边界层流动行为，其中包括纳米颗粒在滑移速度、非均匀产热和磁场影响下向垂直拉伸的可渗透薄片流动。这一目标的动机是由前面引用的纳米流体模型主题的参考文献。对于耦合非线性模型方程的求解，采用谱配点法。本研究的动机是为了更多地了解非牛顿威廉姆森纳米流体问题，并提高我们对它的理解。通过研究这项研究，我们希望增加知识体系，填补知识空白，并可能为各种学科的突破打开大门，包括工程、材料科学和纳米技术。本研究的主要目的是研究滑移速度、磁场、内部产热和粘性耗散对Williamson纳米流体流动行为的影响，并提供一个独特的观点。该研究的新颖性和目的源于这一事实，即它是第一次采用所提出的数值技术来求解所提出的模型。所提出的方法具有许多优点。在谱配点法中使用apap - changhee多项式具有精度高、可用性广、全局逼近、执行效率高、收敛阶高、数值可靠等显著优点。这些优点使它成为一种有效而可靠的数值方法，适用于解决各种数学问题。

本研究组织如下。第2节给出了这个问题的完整描述。在第三节中，我们给出了关于apell - changhee多项式的一些基本概念，并给出了通过acp的近似，并使用单片机进行了程序求解。代码验证在第4节中给出。在第5节中，我们给出了结果和讨论。最后，通过第6节给出了本文的结论。

2 基本模型

在这里，我们考虑纳米流体在温度和浓度恒定的情况下沿着指数拉伸片的二维非牛顿威廉姆森流动。环境浓度和温度的适宜值分别为和。此外，我们假定恒定轴向表面温度大于环境流体温度。在流动模型的基础上，考虑了热泳行为和布朗运动。此外，考虑了新的滑移速度，非均匀产热与布朗运动，热泳特性。速度设为，x轴取拉伸片材方向，其中L为特征长度，为匀速(图1)。进一步，假设片材为多孔，得到吸力速度为。

流动问题的几何示意图

此外，除了非均匀产热假设外，还考虑了以下流体性质作为变量。

(我)粘度

我们假设温度和纳米流体粘度μ的非线性指数函数是相互关联的[24]，即

式中为纳米流体远离薄片的粘度，α为粘度参数。同时，这一关系也解释了纳米流体的黏度行为受到热参数α的影响。通常，对于液体，α被认为是正值。

(ii)导热性

导热性表明了材料的导电性是如何变化的。在这里，我们假设纳米流体导热系数与分布温度的关系如下[24]:

其中ε为导热系数参数，假设较小，为环境导热系数。此外，如果，这个关系表明导热系数是一个常数。

(3)没有不均匀产热

根据非均匀产热与薄板以及环境温度之间的多重相关性，可以观察到，非均匀产热直接表述如下[25]:

式中为运动粘度，和为常数。

使用边界层和Boussinesq估计后的保守方程在考虑上述所有因素的情况下产生[26]

(1) (2) (3) (4)

相关边界条件为[8]:

(5) (6)

重要的是要注意动量方程(2)引入了两个重要的补充:包含可变热粘度和混合对流项。类似地，能量方程(3)包含了粘性耗散项和内热生成项。此外，需要强调的是，式(5)的初始分量表示滑移速度现象，其中流体速度矢量的x轴系数为u, y轴系数为v;， Γ，表示布朗运动的扩散系数、Williamson参数和磁场强度;τ为纳米粒子的有效热容与基液的热容之比，为恒定吸力速度，为多孔介质的渗透率，为热反射扩散系数，σ为电导率，为浓度膨胀系数，为温度膨胀因子，g为重力加速度，为恒压比热，为滑移速度因子，为环境密度。

现在，将非线性偏微分方程(1)~(4)转化为非线性常微分方程(ode)，假设对应的相似度变量如下[26]:

(7) (8)

式中f为无因次流函数，为无因次温度，为无因次浓度。由式(7)可以精确地满足连续性方程(1)。由具有边界约束(5)-(6)的系统(2)-(4)，通过调用变换(7)-(8)，得到以下带有相关边界约束的无量纲ode系统。所以，我们有

(9) (10) (11)

受下列边界限制:

(12) (13)

式中为磁性参数，为滑移速度参数，为吸力参数，为Williamson参数，为普朗特数，为多孔参数，为布朗运动参数，为局部修正Grashof数，为局部Grashof数，为Schmidt数，为Eckert数，为热游参数。据此，Sherwood数、Nusselt数、皮肤摩擦力为[27]:

其中为局部雷诺数。

3.解决方案的过程

3.1 基本的公司型的关于阿普-昌熙多项式

众所周知，常熙多项式通常是用生成函数来定义的(参见[19,22])，

其中为昌熙号，见[19]。这些多项式也可以用下面的形式给出:

式中，分别为第一类斯特林数和欧拉多项式。然而，apile型Changhee多项式是由[28]给出的生成函数定义的

度m的acp定义为

（14）

从式(14)中，很容易得到

（15）

因此，由式(15)可以确认公式如下:

值得注意的是，和。

此外，我们可以证明acp满足以下恒等式:

（16）

设acp的集合，假设

是[28]的有限维子空间。

对于的函数，在Ω中有一个很好的唯一的近似。如果是的唯一近似值，我们可以写出如下的误差估计:

但由于Ω是的闭子空间，根据[29]，我们可以写成，其中表示Ω的正交补，因此我们有，然后，这也意味着。因此，这证实了以下几点:

（17）

式中为内积。

因此，我们可以这样写:

（18）

在哪里

将式(18)代入式(17)得到

同样从(18)中，我们可以看到

（19）

矩阵的定义是

并可由式(16)计算。因此，式(19)中的系数向量可以表示为

在本节中，我们将证明(18)中给出的函数的n阶导数可以通过以下定理近似求得。

定理1

式(18)给出的函数的阶导数可以近似为

(20)

昌熙的号码在哪里，是谁给的

证明

考虑i次的ACP，用(18)，可以得到

在(20)中给出，这就完成了证明。□

3.2 用单片机解决程序

我们将利用单片机对系统(9)-(13)进行数值求解。我们分别用、、和近似，如下所示:

（21）

把(20)和(21)代入(9)-(11)得到

(22) (23) (24)

将前面的方程(22)-(24)在点，进行搭配，可以简化为系数，，，的代数方程组。

另外，将式(21)代入式(12)-式(13)中，边界条件(12)-式(13)表示为:

(25) (26)

其中，和的值可以用迭代公式计算

式(25)-式(26)与式(22)-式(24)共同给出了一个代数方程组。我们将用牛顿迭代法求解这个系统的未知数，，，，。反过来，这将引导我们通过(21)式的代换来计算近似解。

目录

摘要
1 介绍
2 基本模型
3.解决方案的过程
4 代码验证
5 结果与讨论
6 结论
数据和材料的可用性
参考文献
致谢

作者信息
道德声明



搜索
导航

#####

4 代码验证

在本节中，我们将表面摩擦系数的数值与Williamson参数的各种值与Nadeem和Hussain[30]计算的数据进行比较，以证实我们使用谱搭配法获得的数值结果，谱搭配法取决于acp的特性。如表1所示，这些发现与Nadeem和Hussain[30]的文献报道密切相关。因此，我们可以自信地说，这里提供的数据是准确的。

5 结果与讨论

使用SCM建立纳米颗粒的流动、热和传质特性的重要特征的结果如图2至13和表2所示。图2分别描述了磁性参数M如何影响温度、速度和浓度图。由图2可知，当磁场参数较大时，洛伦兹力变强，流体阻力增大，速度减小。此外，还观察到，随着磁性参数的增加，溶质边界层的厚度减小，溶质浓度下降。此外，磁参数的增加似乎改善了温度分布。

(a)和各种M;(b)对于各种M

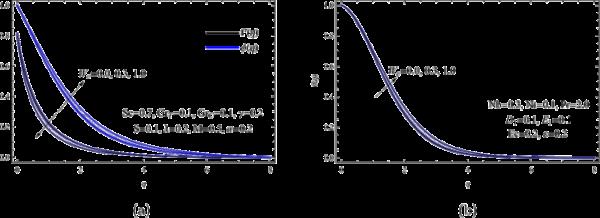
图3显示了滑移速度参数λ不同取值时速度场、温度场和浓度场的变化情况。随着滑移速度参数λ的增大，滑移速度场呈递减趋势，而温度场则呈相反趋势。结果表明，滑移速度参数的增大减小了纳米颗粒的体积摩擦，改善了边界层厚度和浓度分布。从物理上讲，与滑移速度参数相关的纳米流体速度降低可以用滑移流来解释，滑移流指的是固体表面附近的流体以与表面本身不同的速度移动的情况。当纳米颗粒存在于固体表面附近的纳米流体中时，它们会形成一个边界层，影响流体的流动行为。滑移速度参数量化滑移流动，表示流体与固体表面之间的相对速度。

(a)和表示各种λ;(b)为各种λ

对于一个特定的粘度参数α值，它定义了流动行为和热质传递在边界层中的传播，图4显示了速度、温度和浓度曲线。结果表明，随着粘度参数的增大，涂层粘度的提高幅度更大，这与粘度参数增大时流体速度减小有关。黏度参数越大，质量输运和热输运越强，温度场和浓度场增强。从物理上讲，粘度参数衡量流体的流动能力。纳米粒子加入后会改变纳米流体的粘度。因此，纳米流体的速度降低。纳米颗粒的加入改变了流体分子之间的相互作用，整体上增加了纳米流体的粘度。这种增加的黏度导致流体经历更大的内摩擦，从而减缓流动并降低速度。

(a)和各种α;(b)为各种α

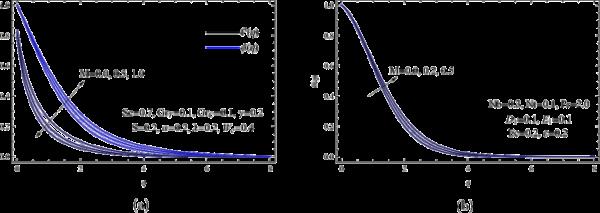
图5检查了Williamson参数对、和分布的影响。与浓度和温度分布相反，速度分布发生了变化。温度和浓度分布随着Williamson参数的增大而增大。这表明，随着纳米颗粒迁移率的增加，纳米流体的导热系数也增加，从而促进了传热传质机制。

(a)和各种;(b)用于各种

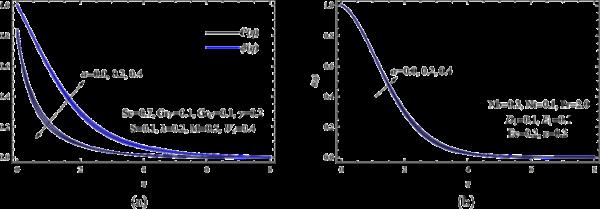
几个多孔参数γ值的速度、浓度和温度分布如图6所示。在这种情况下，提高孔隙参数γ会导致速度分布急剧恶化，尽管温度场和浓度场呈现相反的趋势。此外，多孔参数对热边界层厚度也有一定的改善作用。

(a)和各种γ;(b)不同γ

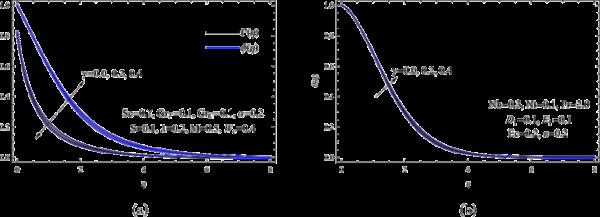
图7显示了提高局部Grashof数如何改善速度剖面。随着局部格拉什夫数的增加，对流机制得到改善，纳米流体的速度也随之增加。相反，温度场和浓度场表现出不同的行为。物理上，格拉什夫数是一个无量纲参数，它捕捉流体流动中浮力和粘性力之间的平衡。以下的物理解释解释了为什么更高的格拉什夫数会导致更快的纳米流体:格拉什夫数的增加表明浮力比粘性力更大。由于温度或密度的变化，流体因此会遇到更强的推力。这种更强大的推力使纳米流体移动得更快，从而改善了对流传热。因此，增加的格拉什夫数导致纳米流体速度增加，鼓励更活跃的流体流动和更好的对流换热。

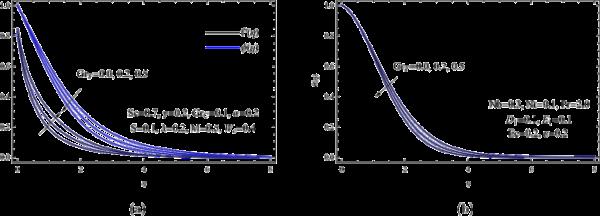
(a)和各种;(b)用于各种

在图8(a)和8(b)中绘制了在层流Williamson纳米流体流动区运行的局部修正Grashof数的速度、温度和浓度分布结果。从图中可以看出，随着局部修正的Grashof数的增加，速度场和边界层厚度都有所改善。此外，对于相同的质量和热输运参数，则显示相反的结果。

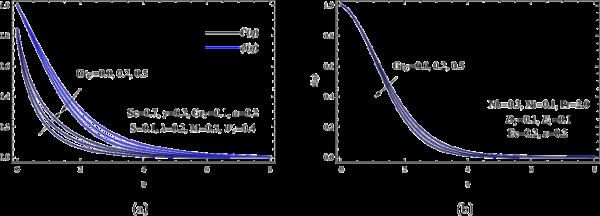
(a)和各种;(b)用于各种

导热系数ε与Williamson纳米流体流动和热质量的关系如图9所示。该图表明，当导热系数参数值较大时，边界层区域的速度、浓度和温度分布本质上是上升的。这是因为纳米流体的导电性随着导热系数的增加而提高。从物理上讲，当涉及到纳米流体时，纳米颗粒的存在可以增加流体的导热系数，这是衡量材料导热能力的一种指标。因此，由于热导率参数的增加，纳米流体表现出更高的温度，这是由于流体传导和散热能力的提高。

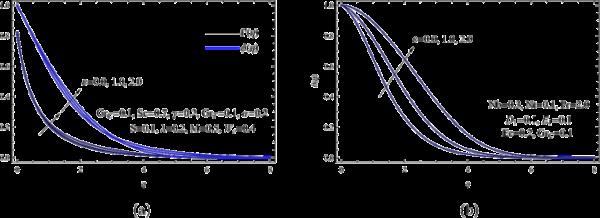
(a)和各种ε;(b)为各种ε

对于不同的热泳参数Nt值，图10描绘了浓度和温度场的变化。已经注意到，随着热泳参数的升高，浓度和温度曲线都升高，因为热泳是一种现象，通过这种现象，小颗粒从热表面被吸引到冷表面，从而导致温度升高。

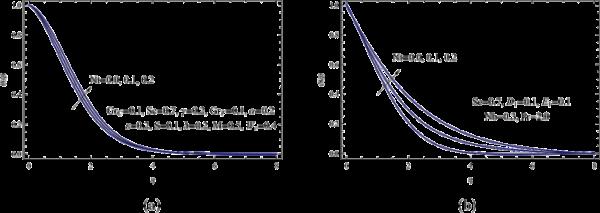
(a)各种Nt;(b)对于各种Nt

图11显示了纳米流体的温度和浓度场如何受到布朗运动参数Nb的影响。该图说明了提高布朗运动参数如何导致流体粒子随机移动，从而提高浓度和温度曲线。

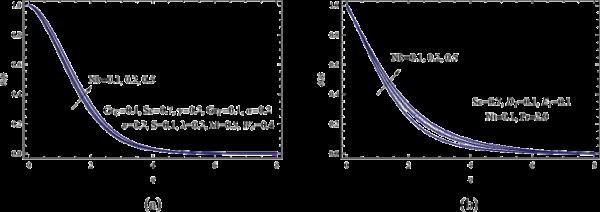
(a)各种Nb;(b)不同Nb

热边界层区域内的温度分布受Eckert数Ec的影响，如图12(a)所示，因为Eckert数的增加加速了动能的运动。因此，流体粒子碰撞更有规律，这导致动能在此过程中转化为热能。结果，温度曲线上升，如图所示。图12(b)显示了与空间相关的热源参数如何影响温度分布。空间热源参数越高，流体温度越高;这一现象在物理上得以维持，因为高值会导致纳米流体的热量产生增加和温度分布增加。

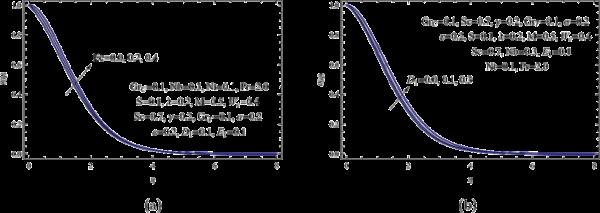
(a)各种Ec;(b)用于各种

温度相关热源参数对温度和浓度分布的影响如图13所示。该图显示了增加温度相关的热源参数如何增加传热传质能力，从而导致纳米流体温度和浓度的增加。

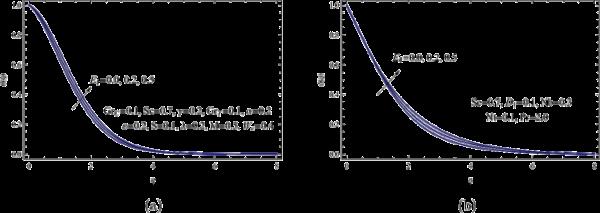
(a)用于各种;(b)用于各种

表2显示了磁场参数、滑移速度参数、局部Grashof数、导热系数参数、热透参数、多孔参数、局部修正Grashof数和Williamson参数改变后的表面摩擦系数、Nusselt数和Sherwood数的变化。很明显，当热导率、Williamson、多孔性、热电泳、局部Grashof和磁性参数较高时，局部努塞尔数下降。局部舍伍德数在同一表中显示为滑移速度、磁场、粘度和孔隙参数的递减函数。重要的是要记住，当滑移速度、粘度参数和导热系数参数值上升时，局部表面摩擦系数下降。然而，对于磁性、多孔性和威廉姆森参数的高值，这种影响是相反的。

6 结论

在这项工作中，非牛顿威廉森纳米流体流动特性引起的垂直指数拉伸片。利用谱配位技术对上述问题进行了数值求解，该方法主要依赖于艾尔型长熙多项式的性质。水流被认为处于稳定状态。Williamson纳米流体流动的滑移速度现象、磁场的影响、热量的产生和粘性耗散都对这项研究的观察产生了影响。使用图形分析来查看和分析嵌入因素的影响。这些数值计算和数学建模具有重要的应用，特别是在冷却操作中。因此，本研究可以明确在工程应用中至关重要的几个基本方面。主要研究结果如下:

1. 1.

   随着黏度、滑移速度、局部格拉什夫数等参数的增大，表面摩擦力减小。

2. 2.

   与磁场、滑移速度和粘度参数对流体运动的影响相反，局部格拉什夫数的增加会导致流体速度加速。

3. 3.

   滑移速度和局部修正的Grashof数增加了Nusselt数，而磁性、Williamson和多孔参数则降低了Nusselt数。

4. 4.

   纳米流体的温度是由磁场和较高水平的局部格拉什夫数控制的。

5. 5.

   随着热泳参数的增大，努塞尔数减小，而粘度参数则呈现相反的趋势。

6. 6.

   变粘度参数、Grashof数、修正Grashof数和导热系数参数的增大导致表面摩擦系数的减小。

7. 7.

   在未来的努力中，通过研究不同变量(如纳米颗粒浓度、孔隙度和化学反应)对非牛顿威廉姆森纳米流体流动行为的影响，将有利于扩大本研究的分析范围。

下载原文档：https://link.springer.com/content/pdf/10.1186/s13661-023-01765-8.pdf